Sem IV IT/BCA Dijkstra's Algorithm
One algorithm for finding the shortest path from a starting node to a target node in a weighted graph is Dijkstra’s algorithm. The algorithm creates a tree of shortest paths from the starting vertex, the source, to all other points in the graph.
Dijkstra’s algorithm, published in 1959 and named after its creator Dutch computer scientist Edsger Dijkstra, can be applied on a weighted graph. The graph can either be directed or undirected. One stipulation to using the algorithm is that the graph needs to have a nonnegative weight on every edge.
How Dijkstra's Algorithm works
Dijkstra's Algorithm works on the basis that any subpath B -> D of the shortest path A -> D between vertices A and D is also the shortest path between vertices B and D.
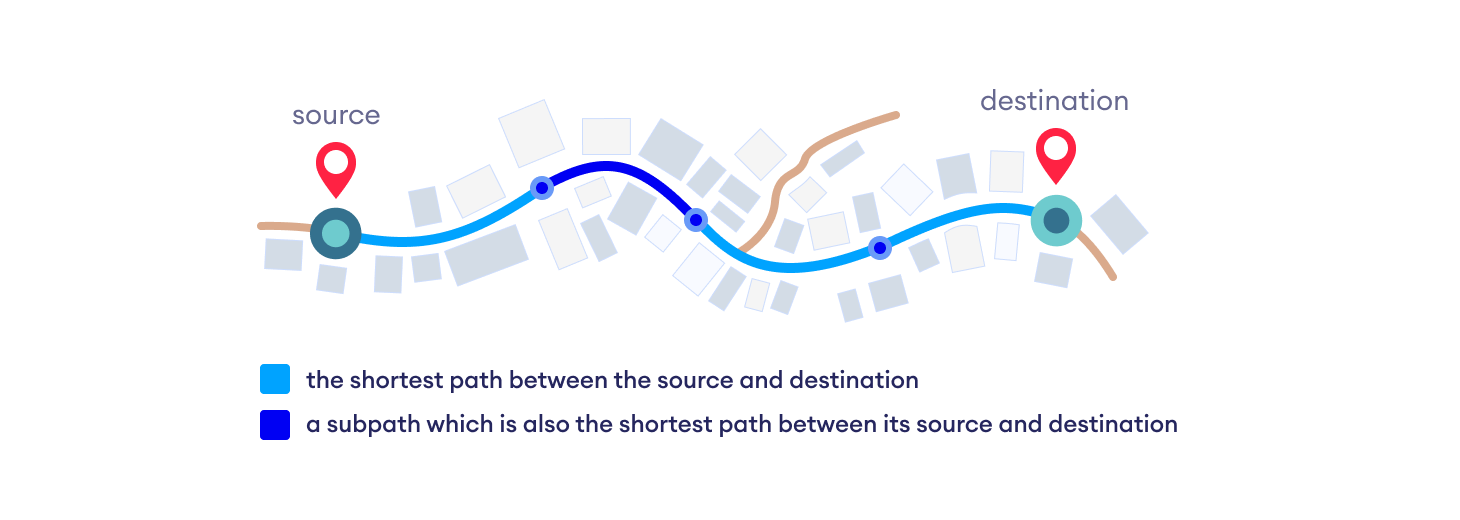 Each subpath is the shortest path
Each subpath is the shortest path
Djikstra used this property in the opposite direction i.e we overestimate the distance of each vertex from the starting vertex. Then we visit each node and its neighbors to find the shortest subpath to those neighbors.
The algorithm uses a greedy approach in the sense that we find the next best solution hoping that the end result is the best solution for the whole problem.
Example of Dijkstra's algorithm
It is easier to start with an example and then think about the algorithm.
 Start with a weighted graph
Start with a weighted graph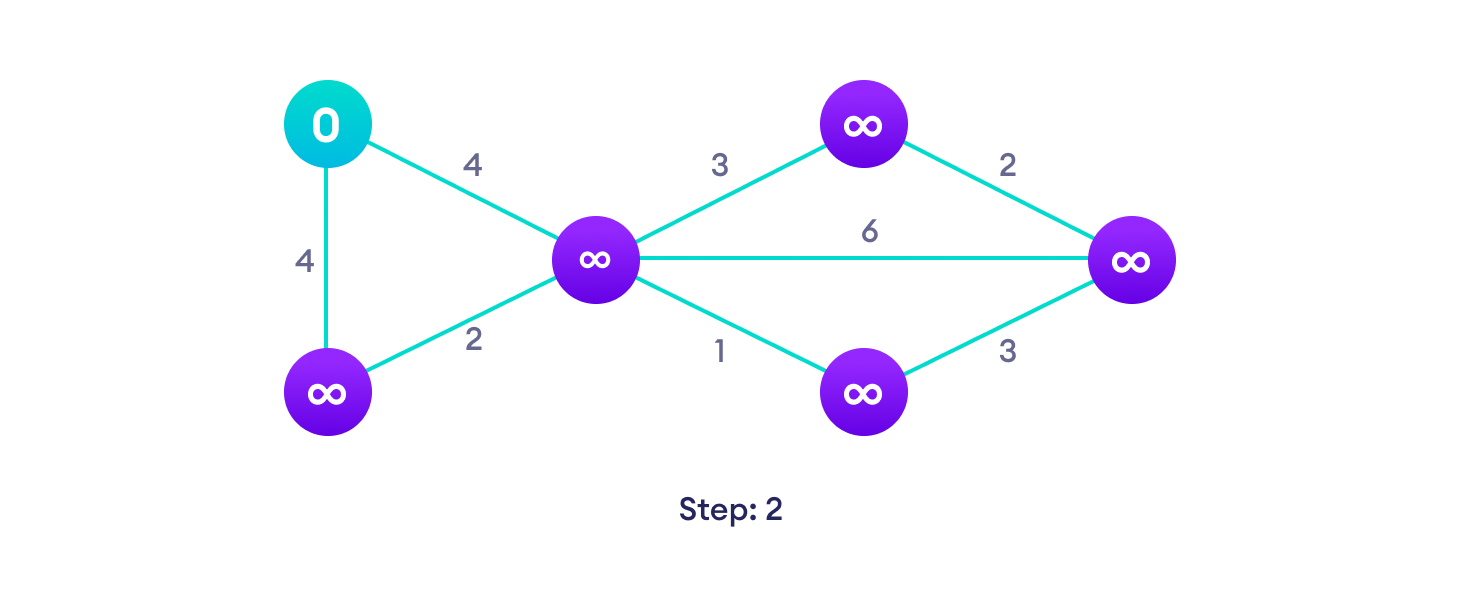 Choose a starting vertex and assign infinity path values to all other devices
Choose a starting vertex and assign infinity path values to all other devices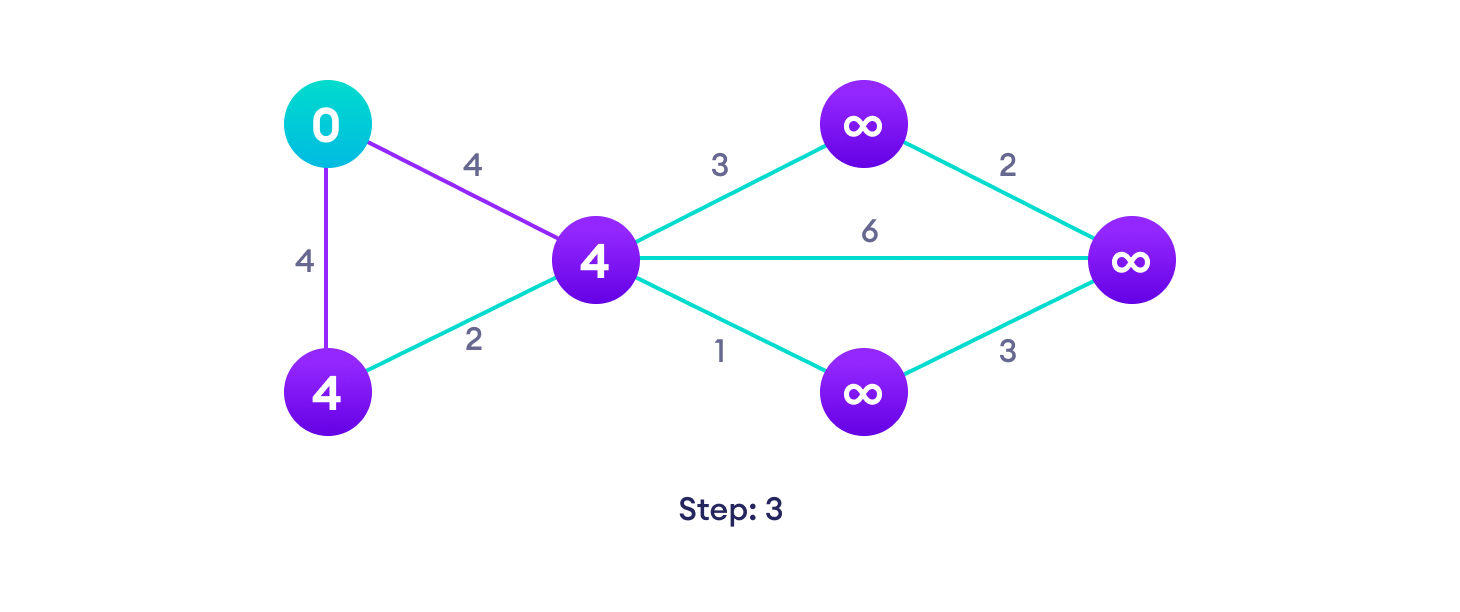 Go to each vertex and update its path length
Go to each vertex and update its path length If the path length of the adjacent vertex is lesser than new path length, don't update it
If the path length of the adjacent vertex is lesser than new path length, don't update it Avoid updating path lengths of already visited vertices
Avoid updating path lengths of already visited vertices After each iteration, we pick the unvisited vertex with the least path length. So we choose 5 before 7
After each iteration, we pick the unvisited vertex with the least path length. So we choose 5 before 7 Notice how the rightmost vertex has its path length updated twice
Notice how the rightmost vertex has its path length updated twice
Repeat until all the vertices have been visited